Traverse Surveying – Definition, Types, Methods, Checks

Definition: Traverse is a series of connecting lines or paths. This process is called traversing.

Let us assume an area and some points over there, connecting all points by traversing through these points for survey of that area is Traverse. 

---

Types of Traverse Surveying

There are two types of traverse surveying.

1. Open Traverse
2. Closed Traverse

Open Traverse

When a series of connected lines extends along a common direction and does not return to the starting point, it is known as an open traverse or (unclosed traverse).

Here ABCDEF represents an open traverse.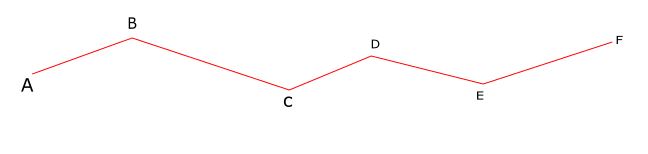

Closed Traverse

When a series of connected lines forms a closed circuit, i.e. when the finishing point meets with the starting point of a survey, it is called a closed traverse.

Closed traverse is suitable for the survey of boundaries of ponds, forests, etc.

Here ABCDE represents a closed traverse.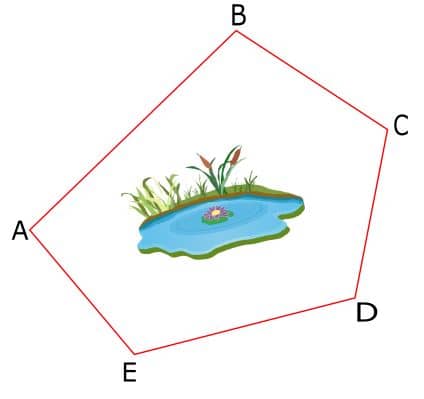

---

Methods of Traversing

There are four different methods of traversing.

1. Chain Traversing
2. Chain and compass Traversing
3. Theodolite Traversing
4. Plane Table Traversing

Chain Traversing

As the name indicate the method of traversing in which the whole work is performed with the chain and tape is called chain traversing.

In chain traversing, there is no angle measurement is used and the directions of the lines are fixed entirely by linear measurements. Angles fixed by linear or tie measurements are known as chain angles.

This method is incompatible for accurate work and is generally used if an angle measuring instruments such as a compass, sextant or theodolite is available.

Chain and Compass Traversing

Chain and compass surveying is also known as a free or loose needle method. In this method of traversing a chain is used for the linear measurements and a compass is used for angular measurements. 

As the compass is used at all stations so that may be subjected to local attraction that might cause an error. So it is not so highly accurate. 

Theodolite Traversing

In Theodolite traversing basically, we have to use the theodolite and we have to attach the compass to the theodolite for angular measurements also we need to use chain or tape for linear measurements. 

There are two methods of theodolite traversing:

1. Fast needle method
2. Measurement of included angles

Fast needle method

If we use the fast needle method then we will measure angles at each and every station along with the angle we also measure the bearing at the first station. In this case, the chances of local attraction are less because we only use the compass at the first station.

Measurement of included angles

In this method, at all stations, we have to measure only the included angles. We don’t use a compass. So it is a more accurate method among all methods.

Plane Table Traversing

In this method, we do not use any theodolite and compass for traversing. Only we have to use a table at site and plot all the points along the traversing and also calculate the linear measurements. 

This is a very easy and quick method of traversing.

---

Plotting a Traverse Survey

We plot the traverse with the help of Latitude and Departures. 

For understanding the terms ‘Latitude’&’Departure’ let’s consider two axes NS and EW also a line AB that makes an angle ‘θ‘ with the NS axis and let ‘l‘ be the length of line AB.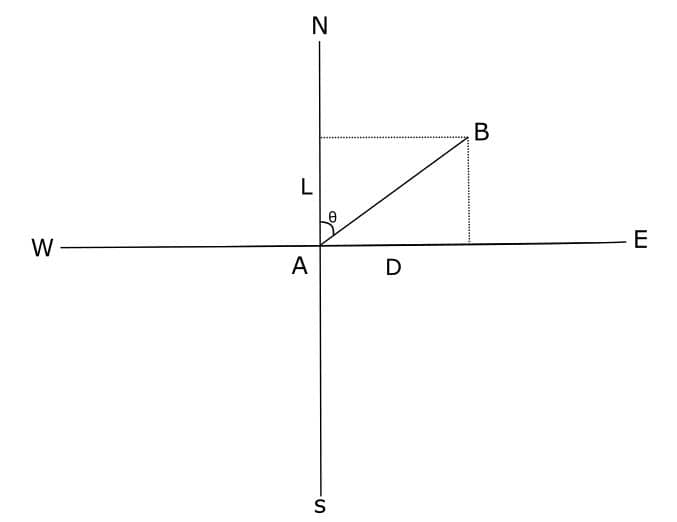

So Projection of a line ‘AB’ on the ‘NS’ axis is called Latitude. 

Latitude, L = lcosθ

Projection of a line ‘AB’ on the ‘EW’ axis is called Departure. 

Departure, D = lsinθ

---

Sign Convention in Traverse Surveying

It is very important to understand the signs for plotting a traverse.

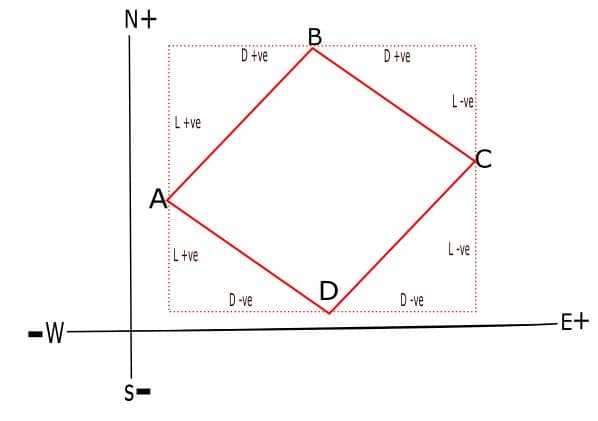
Consider a close Traverse ‘ABCDA’

In the above close traverse ‘ABCDA’ line AB lies on the 1st Quadrant. So latitude (L) is positive (+ve) and Departure is also positive (+ve). 

Line BC lies on the 2nd Quadrant so Latitude L is negative (-ve) and Departure D is (+ve). 

Line CD lies on  the 3rd Quadrant so L is (-ve) 

And departure D is (-ve). 

Line DA lies on the 4th Quadrant so, L is (+ve) 

And departure D is (-ve).

---

Checks in Close traverse

• Sum of  All Latitude is always Zero in close Traverse.
• Sum of all Departures is always zero in close a traverse. 
• Sum of the internal angle is (2n-4)90°
• Sum of the external angle is (2n+4)90°

If the Sum doesn’t come zero then there is some error.

---

Errors in Close Traverse

Suppose if we do not reach the point A after traversing then there is some error and we reach another point.

Let us assume that point ‘E‘. 

And total distance b/w AB is our net error value I. e. ‘e’. 

Let us suppose latitude error value bee_L and departure be e_D.

After knowing these two values we can calculate the net error value. 

# As we got this error while closing the traverse so this is a closing error. 

For calculation of error

We know that:-

The sum of all latitudes is zero i.e.

ΣL= 0

The sum of all departure is zero

ΣD=0

Net error Calculation:

By Pythagoras theorem: e=√(e_L)²+(e_D)²

Error in Direction:

θ= tan^-1(e_D/e_L)

---

Methods for correction of errors

(1) Bowditch Method

There are two assumptions in this method:-

• Errors in linear measurements directly proportional to √l
• Errors in angular measurements are inversely proportional to √l

(a) Correction in latitude of line:

CL₁= l₁/Σl * eL  (corrected L= CL₁+l₁)

Where l₁is the length of the individual line. 

Σl is a sum of all lengths of line

(b) Correction of Departure:

CD₁= l₁/Σl*eD(corrected D=CD₁+D₁)

2) Transit Method

We use this method when angular measurements are more precise than linear measurements. 

(a) Correction for latitude:

CL= L₁/LT *eL

Where LT is  a sum of all latitudes

(b) Correction for Departure:

CD=L₁/LT *eD