Circumcenter of Triangle – All the things in nature represent perfect symmetry. This symmetry can be seen in the physical phenomenon, chemical interactions, Biological transitions and geometrical shapes around us. This symmetry helps us to find the type of interactions between materials.
Let us emphasises geometry. Geometry aids us in determining which materials to utilise and what design to create, as well as playing an important role in the construction process.
Different houses and structures are constructed in various geometric forms to provide a unique appearance as well as adequate ventilation.
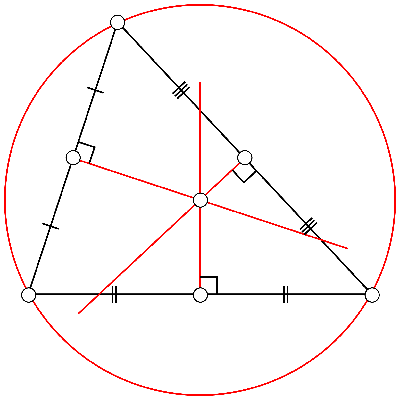
In this post, we will look at the geometry of a triangle, which is one of the geometrical shapes. Triangles have properties such as vertices, sides, edges, and perimeters, but circumcenter is the only attribute that is unique to them.
It allows us to locate the point at where all of a triangle’s perpendicular bisectors intersect. Circumcenter also assists us in determining the centre of triangular objects such as pyramids.
Definition
BYJUS states that
“The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersect. In other words, the point of concurrency of the bisector of the sides of a triangle is called the circumcenter. It is denoted by P(X, Y). The circumcenter is also the centre of the circumcircle of that triangle and it can be either inside or outside the triangle.”
Or
According to CUEMATH
“Circumcenter of triangle is the point where three perpendicular bisectors from the sides of a triangle intersect or meet. The circumcenter of a triangle is also known as the point of concurrency of a triangle.”
Formula
The circumcenter can also be determined by utilising the distance formula to create linear equations. Consider the coordinates of the circumcenter: (X, Y). The circumcenter properties state that (X, Y) is the same distance from each vertex of a triangle.
The formula is as follows if D1 is the distance between the vertex (x1, y1) and the circumcenter (X,Y):
D1= √ [(X−x1)2 + (Y−y1)2]
D2= √ [(X−x2)2 + (Y−y2)2]
D3= √ [(X−x3)2 + (Y−y3)2]
Since D1=D2 and D2=D3, we now have
[(X−x1)2 + (Y−y1)2] = [(X−x2)2 + (Y−y2)2]
Two linear equations are derived from this. The circumcenter coordinates can be found by solving linear equations using the substitution or elimination approach.
Properties of a circumcenter
- The angle of the circumcenter is predictable, whether it is acute, right, or obtuse.
- If the circumcenter is inside the triangle, the triangle is acutely tilted.
- If one of the triangle’s sides is right-angled, the circumcenter is at the hypotenuse.
- Obtuse angled triangle when the circumcenter is outside the triangle.
How do you find the triangle’s circumcenter?
Example 1:
Calculate the circumcenter of triangle whose vertices are (3, 2), (1, 4) and (5, 4).
Step 1: write the provided information
Given: (x1, y1) = (3, 2); (x2, y2) = (1, 4) and (x3, y3) = (5, 4)
Step 2: Calculate the first linear equation by using distance formula we have.
D1 = D2
(X−x1)2 + (Y−y1)2] = [(X−x2)2 + (Y−y2)2
(X−3)2 + (Y−2)2 = (X−1)2 + (Y−4)2
X2+9-6X+Y2+4-4Y = X2+1-2X+Y2+16-8Y
X2-6X+Y2-4Y+13 = X2-2X+Y2-8Y+17
X2-6X+Y2-4Y+13- (X2-2X+Y2-8Y+17) = 0
X2-6X+Y2-4Y+13-X2+2X-Y2+8Y-17) = 0
-4X+4Y-4= 0
-X+Y=1___________1)
Step 3: Calculate the second linear equation by using distance formula we have.
D1 = D3
(X−x1)2 + (Y−y1)2] = [(X−x3)2 + (Y−y3)2
(X−3)2 + (Y−2)2 = (X−5)2 + (Y−4)2
X2+9-6X+Y2+4-4Y = X2+25-10X+Y2+16-8Y
X2-6X+Y2-4Y+13 = X2-10X+Y2-8Y+41
X2-6X+Y2-4Y+13 -(X2-10X+Y2-8Y+41) = 0
X2-6X+Y2-4Y+13 -X2+10X-Y2+8Y-41 = 0
4X+4Y-28=0
4X+4Y=28
Divide both sides by 4
X+Y=7________ (2)
Step 4: Compare equation 1 and 2 to calculate the circumcenter.
By adding equation 1 from 2 we have
2Y = 8
Y = 4
Now by putting the value of Y in 2 we have
X+4=7
X=7-4
X = 3
Hence the coordinates of the circumcenter of a triangle are (3, 4).
Many times, in scientific and mathematical calculations involving complicated operations with intricate numbers, manual computation is not feasible since it takes too long and is prone to mistakes.
So to overcome this problem a Circumcenter calculator is very helpful in order to save valuable time by avoiding these long calculations. To use a circumcenter calculator, follow the steps below.
Step 1: Enter the given values of vertices of the triangle and press calculate button.
Hence the vertices of the circumcenter have been calculated by using this quick method.
Example 2:
Calculate the circumcenter of a triangle whose one vertices is different from the above triangle vertices are (3, 2), (1, 4) and (3, 4).
Step 1: write the provided information
Given: (x1, y1) = (3, 2); (x2, y2) = (1, 4) and (x3, y3) = (3, 4)
Step 2: Calculate the first linear equation
By using distance formula we have
D1 = D2
(X−x1)2 + (Y−y1)2] = [(X−x2)2 + (Y−y2)2
(X−3)2 + (Y−2)2 = (X−1)2 + (Y−4)2
X2+9-6X+Y2+4-4Y = X2+1-2X+Y2+16-8Y
X2-6X+Y2-4Y+13 = X2-2X+Y2-8Y+17
X2-6X+Y2-4Y+13- (X2-2X+Y2-8Y+17) = 0
X2-6X+Y2-4Y+13-X2+2X-Y2+8Y-17) = 0
-4X+4Y-4= 0
-X+Y=1___________1)
Step 3: Calculate the second linear equation
By using distance formula we have
D1 = D3
(X−3)2 + (Y−2)2 = (X−3)2 + (Y−4)2
X2+9-6X+Y2+4-4Y = X2+9-6X+Y2+16-8Y
X2-6X+Y2-4Y+13 = X2-6X+Y2-8Y+25
X2-6X+Y2-4Y+13 -(X2-6X+Y2-8Y+25) = 0
4Y-12=0
4Y=12
Divide both sides by 4
Y=3________ (2)
Step 4: Put the value of Y in equation 1 to find the value of X.
By adding equation 1 from 2 we have
-X+3=1
-X= 1-3
-X=-2
X=2
Hence the coordinates of the circumcenter of the triangle are (2, 3).
Summary:
The point at which the centre of the circle that will be generated is tangent to all three vertices of a triangle is called the circumcenter. Outside of (circumscribed by) the triangle will be the circle. The circumcenter is the place where the triangle’s three perpendicular bisectors connect. All three triangle vertices are equidistant from the circumcenter. The circle’s radii will contact each of the circle’s three vertices.
Geometrical shapes plays an important role in the field of mathematics. Any geometrical form can be calculated manually or with the use of a calculator, such as a circumcenter calculator. These equations allow us to calculate the area of any physical project, such as creating a commercial market or a residential.
Also Read: All Formula of Civil Engineering PDF Download

Leave a comment