Elementary Profile of Gravity Dam | Difference Between Elementary and Practical Profile

Elementary profile of gravity dam

Gravity dam is subject to horizontal pressure because of water and also another force acting is self-weight of the dam. So in this case, if the dam is subject to horizontal pressure of water and its self-weight then the elementary profile of the gravity dam would be a right-angled triangle. Elementary profile of the dam is also known as the theoretical profile of the gravity dam.

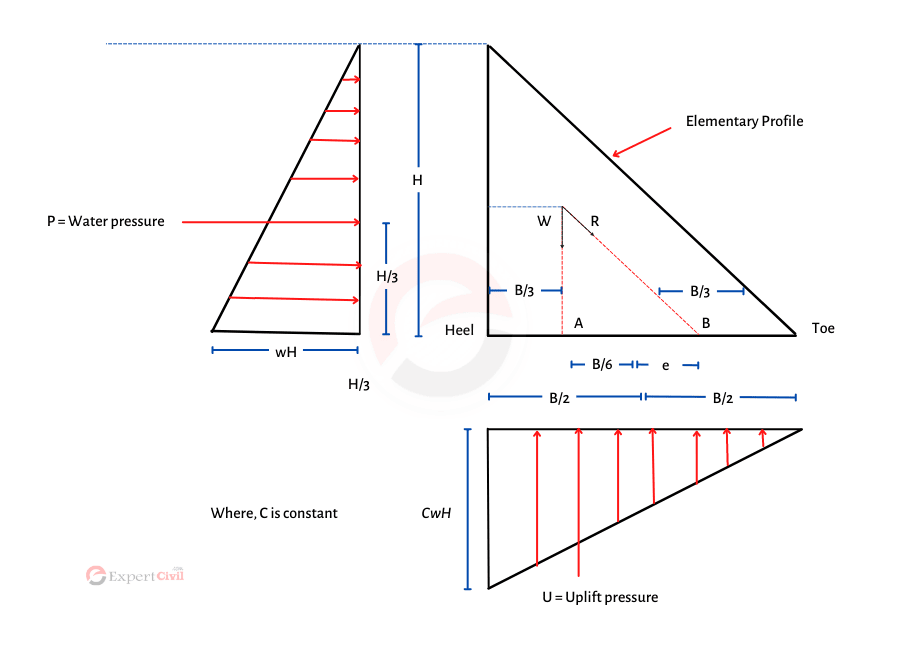
• Thickness of gravity dam at the base would be maximum because of that their pressure of water means hydrostatic pressure will be maximum.
• Thickness of gravity dam at water surface level would be zero because of that there no such water (hydrostatic) pressure is there.
• Hydrostatic pressure variation from bottom to surface level is linear so the variation in elementary profile from top surface level to base level will be also linear.
• This triangular elementary profile of gravity dam would give maximum stabilization against any overturning forces and also without causing tension condition in case of the reservoir is empty. Because here weight of the dam act as b/3 from the upstream vertical face.
• Another triangular elementary profile rather than a right-angled triangular profile gives more stabilization than this profile but it may create tension at the toe of the dam and result in overturning.

The forces acting on gravity dam while determining the elementary profile are taken into account as follow:

1. Self-weight of the dam (W)

\((\text{But},\text{ }W=\frac{\text{1}}{\text{2}}bH\rho w)\)

• Where, W= self-weight of the dam
• b=Base width of the dam
• H=Height of the elementary profile of gravity dam
• ρ= Specific density of the material which used in the dam
• w= Unit weight/ density of water

It affects vertically downward and at a C.G. of the dam.

2. Water pressure or hydrostatic pressure (P)

\(P=\frac{1}{2}w{{H}^{2}}\)

• Where, P= Horizontal water pressure
• w= Unit weight or density of water
• H= Height of the elementary profile of the gravity dam

Force P acts horizontally at 1/3^rd height of elementary profile.

3. Uplift Pressure (U)

\(U=\text{ }\frac{1}{2}cwbH\)

• Where, U= Uplift pressure
• c= Uplift pressure intensity coefficient
• w= Unit weight or density of water
• b= Base width of the elementary profile of the dam
• H= height of elementary profile of gravity dam

Uplift pressure acts vertically upwards and as result, it reduces the gravity load of the dam.

Elementary profile of gravity dam derivation

The elementary profile of the gravity dam and its derivation will be derived as follow:
The elementary profile is based on only external pressure act on the dam which acts on the upstream side, the width of the dam at water surface level will be zero and maximum(B) at the base of the dam.

it will be based on two conditions

1. Reservoir is empty
2. Reservoir is full

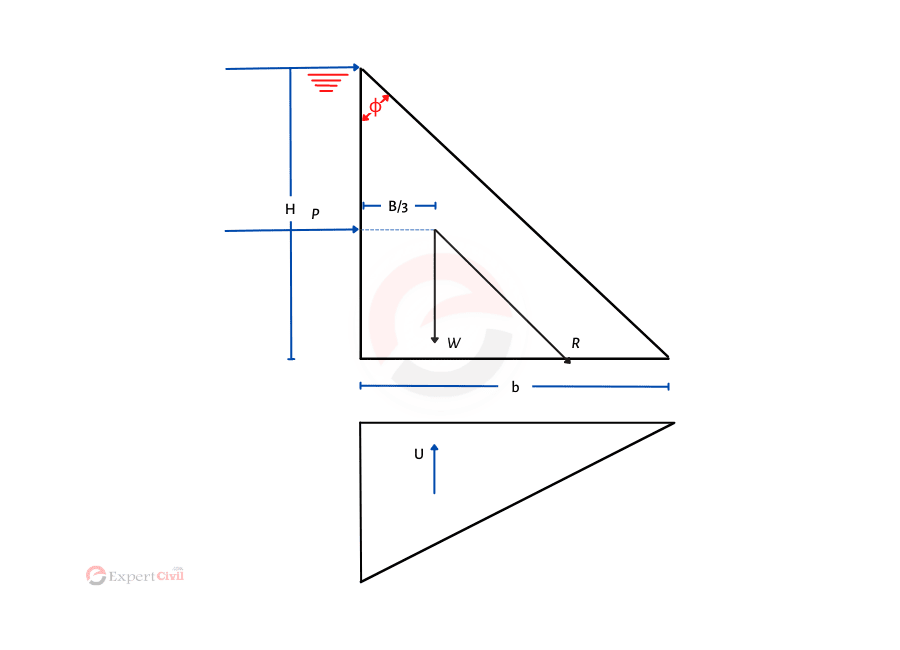
First when the reservoir is in empty condition,

When the reservoir is empty on self-weight(W) of the dam is acting as a force at a B/3 distance from the point of the heel. So action line of W will create a maximum stabilizing moment without causing tension or overturning in this condition.

So the stress distribution in this condition in a vertical manner,

\[\frac{P\max }{P\min }=\frac{\sum{Y}}{B}\left[ 1\pm \frac{6e}{B} \right]\]

\(\text{Where},\sum{Y}=W\ \text{and }e=B/6\)

\[\frac{P\max }{P\min }=\frac{W}{B}\left[ 1\pm \frac{6\times B/6}{B} \right]\]

\(\text{Hence},\text{ }{{P}_{max}}=\frac{2W}{B}~\text{and }{{P}_{min}}=0\)

So maximum stress will be 2W/B and at toe vertical stress as resultant will be zero nearer to heel.

Second when the reservoir is full,

In this condition based width will be counted by

1. Taken account of all the resultant forces, where P and U act at 1/3^rd of an outermost middle point.
2. When safe sliding of the dam.

First, considering all the moments at 1/3^rd point,

\[W\left( \frac{B}{3} \right)-U\left( \frac{B}{3} \right)-\frac{\rho H}{3}=R\times 0\]

\[\left( W-U \right)\left( \frac{B}{3} \right)-\frac{\rho H}{3}=0\]

\(\begin{align}
& \text{But},\text{ }W=\text{ }\frac{1}{2}\text{ }bH\rho w \\
& \text{Here, }\rho =\text{ Specific gravity} \\
& w=\text{ unit weight of water}=\text{ }9.81\text{ }kN/{{m}^{3}} \\
\end{align}\)

\(U=\frac{1}{2}CwbH\)

\(\begin{align}
& \text{Here, if }C=1\text{ then, }B=\ \frac{H}{\mu (\rho -1)}\ldots .\left( 1 \right)~~ \\
& \text{And, if }C=0\text{ then, }\!\!~\!\!\text{ }\ B\ge \frac{H}{\mu \rho }\ldots .\left( 2 \right)~ \\
\end{align}\)

So a value of B will be chosen whichever comes greater from equations 1 & 2.

Base width of the elementary profile of gravity dam

Base width of the elementary profile of the gravity dam can be determined by two conditions:

1. On a stress basis
2. On basis of stability of sliding

1. On a stress basis

As we all know when the reservoir is empty no tension is developed and resultant forces pass through the middle third point and create the moment

So taken account of that considering all the moments,

\[\left(\frac{1}{2} B H \rho w \times \frac{B}{3}\right)-\left(\frac{1}{2} w H^{2} \times \frac{H}{3}\right)-\left(\frac{1}{2} C w B H \times \frac{B}{3}\right)=0\]

\[\frac{1}{2} \times \frac{H}{3} \times w\left(\rho B^{2}-H^{2}-C B^{2}\right)=0\]

So, by solving the equation \(B=\frac{H}{\sqrt{\rho-C}}\)
If uplift pressure intensity coefficient \(C=1\), then \(B=\frac{H}{\sqrt{\rho-1}}\)
And if \(\mathrm{C}=0\), then \(\mathrm{B}=\frac{H}{\sqrt{\rho}}\)

2. On basis of stability of sliding

The horizontal force causing sliding should be equal to or less than the frictional force which resists sliding of the dam.

The Most difficult condition is when both the forces are of the same amount.

\(\begin{aligned}
&\rho=\mu(W-U) \\
&\frac{1}{2} w H^{2}=\mu\left(\frac{1}{2} b H \rho w-\frac{1}{2} C b w H\right) \\
&H=\mu(b \rho-C b) \\
&H=\mu b(\rho-C) \\
&\text { So, } b=\frac{H}{\mu(\rho-C)}
\end{aligned}\)

If C (uplift pressure coefficient is neglected) then, \(b=\frac{H}{\mu \rho }\)

Hence from both the cases stress and sliding condition whichever value comes greater, it will be considered as the value of base width.

Also Read: Diversion Headworks

Difference between elementary and practical profile of gravity dam

Elementary profile of gravity dam	Practical profile of gravity dam
The Elementary profile shape is a perfect right-angle triangle.	The Shape of the practical profile will not be exactly a right-angle triangle.
There is no such width is provided on top of the dam.	Here the thick top is provided on top of the dam which works as a roadway.
In the elementary profile, no freeboard provision is adopted.	After modification in practical profile, some freeboard is provided to the dam which increases the height of the dam.
There is no such additional stress is acting in this profile.	Due to extra height and top thick section additional stress is acting on the dam section.
The Thickness will be zero at water surface level so the hydrostatic pressure is zero at top surface level.	At water surface level thickness would be there so the hydrostatic pressure will not be zero at top surface level.

Question and Answer